1. Inercioīda pārvietojums![]()
![]() Inercioīds ir sarežģīta mehāniska sistēma [3]. Tā kustību ietekmē daudzi nosacījumi, kā piemēram, atsvaru rotācijas leņķiskā ātruma maiņa paātrinošā, palēninošā sektorā, inercioīda masa, rotējošā mehānisma rādiuss u.c. Uz tā masas centru darbojas kāds spēks, kura ietekmē tas pārvietojas, gan uz priekšu, gan atpakaļ. Rakstā [1] tika iegūtas šī pāvietojuma skaitliskās izteiksmes inercioīda kustībā, neņemot vērā berzi, kā ari tā pārvietojumi berzes spēku ietekmē, pie kam šie pārvietojumi aprēķināti inercioīda kustības vienā taktī, gan uz priekšu, gan atpakaļ. Tādējādi šīs skaitliskās vērtības var uzskatīt par vidējām vērtībām, jo reāla inercioīda kustībā katrā taktī šis vērtības var būt atšķirīgas dažādu citu faktoru ietekmē, kā arī aprēķinos tika pieņemts, ka pārvietojums ir tieši proporcionāls inercioīda vienas takts gājiena laika kvadrātam, kas atbilst klasiskam kinemātikas priekštatam par materiāla punkta vienmērīgi paātrinātu kustību. Šīs formulas ir sekojošas:
Inercioīds ir sarežģīta mehāniska sistēma [3]. Tā kustību ietekmē daudzi nosacījumi, kā piemēram, atsvaru rotācijas leņķiskā ātruma maiņa paātrinošā, palēninošā sektorā, inercioīda masa, rotējošā mehānisma rādiuss u.c. Uz tā masas centru darbojas kāds spēks, kura ietekmē tas pārvietojas, gan uz priekšu, gan atpakaļ. Rakstā [1] tika iegūtas šī pāvietojuma skaitliskās izteiksmes inercioīda kustībā, neņemot vērā berzi, kā ari tā pārvietojumi berzes spēku ietekmē, pie kam šie pārvietojumi aprēķināti inercioīda kustības vienā taktī, gan uz priekšu, gan atpakaļ. Tādējādi šīs skaitliskās vērtības var uzskatīt par vidējām vērtībām, jo reāla inercioīda kustībā katrā taktī šis vērtības var būt atšķirīgas dažādu citu faktoru ietekmē, kā arī aprēķinos tika pieņemts, ka pārvietojums ir tieši proporcionāls inercioīda vienas takts gājiena laika kvadrātam, kas atbilst klasiskam kinemātikas priekštatam par materiāla punkta vienmērīgi paātrinātu kustību. Šīs formulas ir sekojošas: ![]()
![]()
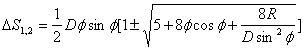 (1.1)
(1.1)
![]()
![]()

![]() (1.2)
(1.2)
kur ΔS-pārvietojums,![]() ,
, ![]() - paātrinošā, palēninošā sektora leņķis, R-inercioīda rotējošās daļas rādiuss. Uzdodot pētāmā inercioīda parametrus D=0,011m,
- paātrinošā, palēninošā sektora leņķis, R-inercioīda rotējošās daļas rādiuss. Uzdodot pētāmā inercioīda parametrus D=0,011m, ![]() =50
=50![]()
![]() ,
, ![]() =30
=30![]() ,R=0,06m, F=0,07N,
,R=0,06m, F=0,07N, ![]() =0,08s, m=0,06kg, M=0,53 kg, pēc formulas (1.1) aprēķina inercioīda pārvietojumu vidējas vērtības vienā taktī, gan tā kustībā uz priekšu, gan atpakaļ. Šie skaitļi ir šādi:
=0,08s, m=0,06kg, M=0,53 kg, pēc formulas (1.1) aprēķina inercioīda pārvietojumu vidējas vērtības vienā taktī, gan tā kustībā uz priekšu, gan atpakaļ. Šie skaitļi ir šādi:![]() S
S![]() =0,037m,
=0,037m,![]() 0,0179m. Atņemot šos skaitļus vienu no otra, iegūst inercioīda vidējo pārvietojumu viena cikla laikā t.i.
0,0179m. Atņemot šos skaitļus vienu no otra, iegūst inercioīda vidējo pārvietojumu viena cikla laikā t.i.![]() .0,019m. Līdzīgi iegūst skaitļus no formulas (1.2), kuri ir nedaudz mazāki
.0,019m. Līdzīgi iegūst skaitļus no formulas (1.2), kuri ir nedaudz mazāki ![]() =0,023m,
=0,023m,![]() =0,015m. Pie maziem berzes spēkiem var izmantot formulu (1.1). Tālāk aplūkojam eksperimentā iegūto līkni, kas iegūta, ja inercioīds pārvietojas vairākās taktīs. Šajā grafikā uz x-ass ir atlikts taktu (atsvaru pilnu apgriezienu periodu) skaits, kur vienas takts periods atbilst T=1,5 s. Uz y-ass atlikts vidējais pārvietojums (cm) vienā taktī, kas ir robežās no 1,5 – 3 cm. Grafiks uzņemts inercoīda kustībai pa virsmu, kur berzes spēks ir
=0,015m. Pie maziem berzes spēkiem var izmantot formulu (1.1). Tālāk aplūkojam eksperimentā iegūto līkni, kas iegūta, ja inercioīds pārvietojas vairākās taktīs. Šajā grafikā uz x-ass ir atlikts taktu (atsvaru pilnu apgriezienu periodu) skaits, kur vienas takts periods atbilst T=1,5 s. Uz y-ass atlikts vidējais pārvietojums (cm) vienā taktī, kas ir robežās no 1,5 – 3 cm. Grafiks uzņemts inercoīda kustībai pa virsmu, kur berzes spēks ir ![]() =0,07N.
=0,07N.
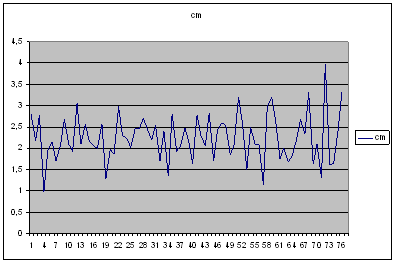
2.zīm.
2. Inercioīda vilcējspēks.
Tika veikti eksperimenti ar kravas vilkšanu uz dažādām virsmām pie atšķirīgiem berzes koeficientiem. Viena virsma bija pulēts akmens galds, bet otra abrazīva virsma. Eksperimentāli noteica berzes spēku inercioīdam ar vienu virsmu, pēc tam ar otru. Pierādījās, ka inercioīdam ir vilcējspēks. Eksperientāli noteica inercioīda berzes spēku uz abām virsmām. To skaitliskās vērtības ![]() =0,068N,
=0,068N,![]() =0,147N. Tālāk eksperimentā noteica ratiņu berzes spēku uz abām virsmām:
=0,147N. Tālāk eksperimentā noteica ratiņu berzes spēku uz abām virsmām:![]() =0,0294N,
=0,0294N,![]() =0,0686N. Zinot šos lielumus, bija iespējams noteikt rites berzes koeficientus inercioīdam un ratiņiem ar apskatāmajām virsmām:
=0,0686N. Zinot šos lielumus, bija iespējams noteikt rites berzes koeficientus inercioīdam un ratiņiem ar apskatāmajām virsmām:![]() =0,0000157m,
=0,0000157m,![]() =0,0000338m., atbilstoši
=0,0000338m., atbilstoši ![]() =0,0000333m,
=0,0000333m,![]() =0,0000777m. Šie koeficienti nepieciešami tālākos aprēķinos. Tālāk apskata sistēmu, kurā inercioīds saistīts ar ratiņiem. Sistēma atrodas miera stāvoklī, ja uz inercioīdu un ratiņiem ar kravu visi darbojošies spēki summā ir nulle. Var uzrakstīt sekojošus vienādojumus:
=0,0000777m. Šie koeficienti nepieciešami tālākos aprēķinos. Tālāk apskata sistēmu, kurā inercioīds saistīts ar ratiņiem. Sistēma atrodas miera stāvoklī, ja uz inercioīdu un ratiņiem ar kravu visi darbojošies spēki summā ir nulle. Var uzrakstīt sekojošus vienādojumus:
![]() (2.1)
(2.1)
![]() (2.2)
(2.2)
vai arī ![]() (2.3)
(2.3)
kur ![]() -vilcējspēks,
-vilcējspēks,![]() -inercioīda riteņu berzes spēks ar apskatāmajām virsmām,
-inercioīda riteņu berzes spēks ar apskatāmajām virsmām,![]() -ratiņu riteņu rites berzes koeficients ar apskatāmajām virsmām, M-ratiņu masa, m-uzkrautā smaguma uz ratiņiem masa, R-ratiņu riteņu rādiuss., g-brīvās krišanas paātrinājums. Ja uzdod skaitliskās vērtības M=0,135 kg, m=1,6kg, m=4kg, R=0,06m, g=9,81
-ratiņu riteņu rites berzes koeficients ar apskatāmajām virsmām, M-ratiņu masa, m-uzkrautā smaguma uz ratiņiem masa, R-ratiņu riteņu rādiuss., g-brīvās krišanas paātrinājums. Ja uzdod skaitliskās vērtības M=0,135 kg, m=1,6kg, m=4kg, R=0,06m, g=9,81![]() , no vienādojuma (2.3) iegūst inercioīda vilcējspēka skaitliskās vērtības uz abām virsmām
, no vienādojuma (2.3) iegūst inercioīda vilcējspēka skaitliskās vērtības uz abām virsmām ![]() . Uz abām virsmām spēki ir vienādi. Apskatam eksperimentā iegūtos grafikus:
. Uz abām virsmām spēki ir vienādi. Apskatam eksperimentā iegūtos grafikus:
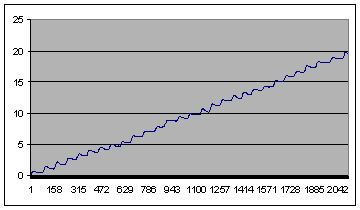
3.zīm.
Šajā grafikā redzams raksturīgais inercioīda pārvietojums, ja uz ratiņiem uzkrauts smagums 1kg. Uz x-ass atlikts laiks ms. Uz y-ass inercioīda pārvietojums cm.
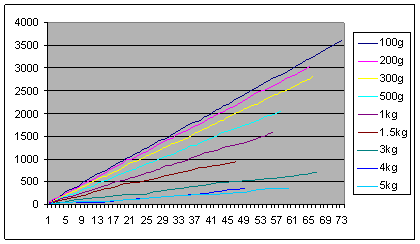
4.zīm.
Šajos grafikos attēlots inercioīda efektīvais pārvietojums, atkarībā no uz ratiņiem novietotā smaguma. No grafikiem redzams, ka pie masas m=4kg inercioīds praktiski vairs nepārvietojas.



