Šis raksts ir turpinājums autora iepriekšējam rakstam [1], kurā tika veikts mēģinājums izskaidrot V.Tolčina inercoīda masas centra kustību. Rakstā [1] tika iegūtas inercioīda pārvietojuma formulas, kā arī tika izvirzīta hipotēze par GEM lauka eksistenci, kurš formējas inercioīda atsvaru paātrinātā, palēninātā kustībā. Izmantojot šo hipotēzi bija iespējams aprēķinos iegūt precīzākas inercioīda pārvietojuma skaitliskās vērtības, atbilstošas eksperimentālām. Tomēr netika noskaidrots kustības cēlonis. Izrādās, ka problēma ir daudz nopietnāka un jautājums par to, kā inerces spēki var veikt darbu, lai pārvietotu inercioīdu, skar dažu dziļāku teorētiskās mehānikas jautājumu izpratni. Tā piemēram, uz mehānikas bāzes attīstījās citas fizikas nozares ar jauniem jēdzieniem. Elektrodinamikā parādās elektromagnētiskais lauks, kas brīvi izplatās telplaikā. Mehānikā pazīstams tikai gravitācijas lauks, caur kuru mijiedarbojas masīvie ķermeņi, jeb telplaika liekums. Analoģiju starp mehāniku un elektrodinamiku var izmantot dažādu neskaidru mehānikas problēmu risināšanā. Tā piemēram bezatbalsta inerces dzinēju, tādiem kā inercioīds, pētījumos. Tomēr, neskatoties uz šādu iespēju, vērā jāņem tas, ka var pastāvēt iespēja tam, ka mehānikas attīstības gaitā no redzes loka izlaisti kādi svarīgi principi. Tā piemēram, neinerciālo atskaites sistēmu mijiedarbība ar ārējiem laukiem, īpaši gravitācijas lauku. Pētot inercioīdu no inerciālās atskaites sistēmas, nevar īsti saprast kādā veidā inerces spēki spēj ietekmēt inercioīda masas centru, jo inerces spēki nav reāli spēki. Arī III Ņūtona likums uz inerces spēkiem nav attiecināms, un mehānika noliedz bezatbalsta inerces dzinēju iespējamību, jo vienīgie reālie spēki ir berzes spēki. Tomēr pēc analoģijas ar elektrodinamiku,var pieņemt, ka inerces spēki rada kādu lauku, līdzīgu elektromagnētiskajam, un kuru var aprakstīt ar Maksvela vienādojumiem [2], kaut būtībā tas nav lauks parastā izpratnē, bet teorētiska konstrukcija, lai varētu pierādīt kādas teorētiskās mehānikas teorēmas. Piemēram enerģijas integrāļa eksistence rotācijas kustībā [2]. Ja rotācijas leņķiskais ātrums ir nemainīgs, tad tāds integrālis eksistē. Ja leņķiskais ātrums mainīgs, tad tādā neinerciālā atskaites sistēmā pilnā mehāniskā enerģija var arī nesaglabāties. Lai novērstu šādu nesaskaņu šajā rakstā tiek piedāvāts tas, ka cirkulējošais inerces lauks ar savu iedarbību spēj izmainīt lokāli ārējo Zemes gravitācijas lauku lokālā apgabalā tā, ka šo abu lauku cirkulācija summā rada gradienta lauku, t.i. tādu, kuram eksistē enerģijas integrālis.
Šajā rakstā būs parādīta iespēja noskaidrot inercioīda kustības cēloni. NEPTA projektu programmas ietvaros tika veikti eksperimenti ar Māliņa konstrukcijas inecioīdu (1.zīm), aprīkotu ar elektroniku, ar kuras palīdzību no inercioīda tiek pārraidīti eksperimentālie dati uz datoru. Tā kā eksperimentu sērija turpinās, apskatāmajā rakstā tiks izmantota daļa no eksperimentiem, pietiekošiem, lai pamatotu teorētiskās konstrukcijas.

1.zīm.
1. Inercioīda pārvietojums![]()
![]() Inercioīds ir sarežģīta mehāniska sistēma [3]. Tā kustību ietekmē daudzi nosacījumi, kā piemēram, atsvaru rotācijas leņķiskā ātruma maiņa paātrinošā, palēninošā sektorā, inercioīda masa, rotējošā mehānisma rādiuss u.c. Uz tā masas centru darbojas kāds spēks, kura ietekmē tas pārvietojas, gan uz priekšu, gan atpakaļ. Rakstā [1] tika iegūtas šī pāvietojuma skaitliskās izteiksmes inercioīda kustībā, neņemot vērā berzi, kā ari tā pārvietojumi berzes spēku ietekmē, pie kam šie pārvietojumi aprēķināti inercioīda kustības vienā taktī, gan uz priekšu, gan atpakaļ. Tādējādi šīs skaitliskās vērtības var uzskatīt par vidējām vērtībām, jo reāla inercioīda kustībā katrā taktī šis vērtības var būt atšķirīgas dažādu citu faktoru ietekmē, kā arī aprēķinos tika pieņemts, ka pārvietojums ir tieši proporcionāls inercioīda vienas takts gājiena laika kvadrātam, kas atbilst klasiskam kinemātikas priekštatam par materiāla punkta vienmērīgi paātrinātu kustību. Šīs formulas ir sekojošas:
Inercioīds ir sarežģīta mehāniska sistēma [3]. Tā kustību ietekmē daudzi nosacījumi, kā piemēram, atsvaru rotācijas leņķiskā ātruma maiņa paātrinošā, palēninošā sektorā, inercioīda masa, rotējošā mehānisma rādiuss u.c. Uz tā masas centru darbojas kāds spēks, kura ietekmē tas pārvietojas, gan uz priekšu, gan atpakaļ. Rakstā [1] tika iegūtas šī pāvietojuma skaitliskās izteiksmes inercioīda kustībā, neņemot vērā berzi, kā ari tā pārvietojumi berzes spēku ietekmē, pie kam šie pārvietojumi aprēķināti inercioīda kustības vienā taktī, gan uz priekšu, gan atpakaļ. Tādējādi šīs skaitliskās vērtības var uzskatīt par vidējām vērtībām, jo reāla inercioīda kustībā katrā taktī šis vērtības var būt atšķirīgas dažādu citu faktoru ietekmē, kā arī aprēķinos tika pieņemts, ka pārvietojums ir tieši proporcionāls inercioīda vienas takts gājiena laika kvadrātam, kas atbilst klasiskam kinemātikas priekštatam par materiāla punkta vienmērīgi paātrinātu kustību. Šīs formulas ir sekojošas: ![]()
![]()
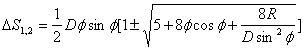 (1.1)
(1.1)
![]()
![]()

![]() (1.2)
(1.2)
kur ΔS-pārvietojums,![]() ,
, ![]() - paātrinošā, palēninošā sektora leņķis, R-inercioīda rotējošās daļas rādiuss. Uzdodot pētāmā inercioīda parametrus D=0,011m,
- paātrinošā, palēninošā sektora leņķis, R-inercioīda rotējošās daļas rādiuss. Uzdodot pētāmā inercioīda parametrus D=0,011m, ![]() =50
=50![]()
![]() ,
, ![]() =30
=30![]() ,R=0,06m, F=0,07N,
,R=0,06m, F=0,07N, ![]() =0,08s, m=0,06kg, M=0,53 kg, pēc formulas (1.1) aprēķina inercioīda pārvietojumu vidējas vērtības vienā taktī, gan tā kustībā uz priekšu, gan atpakaļ. Šie skaitļi ir šādi:
=0,08s, m=0,06kg, M=0,53 kg, pēc formulas (1.1) aprēķina inercioīda pārvietojumu vidējas vērtības vienā taktī, gan tā kustībā uz priekšu, gan atpakaļ. Šie skaitļi ir šādi:![]() S
S![]() =0,037m,
=0,037m,![]() 0,0179m. Atņemot šos skaitļus vienu no otra, iegūst inercioīda vidējo pārvietojumu viena cikla laikā t.i.
0,0179m. Atņemot šos skaitļus vienu no otra, iegūst inercioīda vidējo pārvietojumu viena cikla laikā t.i.![]() .0,019m. Līdzīgi iegūst skaitļus no formulas (1.2), kuri ir nedaudz mazāki
.0,019m. Līdzīgi iegūst skaitļus no formulas (1.2), kuri ir nedaudz mazāki ![]() =0,023m,
=0,023m,![]() =0,015m. Pie maziem berzes spēkiem var izmantot formulu (1.1). Tālāk aplūkojam eksperimentā iegūto līkni, kas iegūta, ja inercioīds pārvietojas vairākās taktīs. Šajā grafikā uz x-ass ir atlikts taktu (atsvaru pilnu apgriezienu periodu) skaits, kur vienas takts periods atbilst T=1,5 s. Uz y-ass atlikts vidējais pārvietojums (cm) vienā taktī, kas ir robežās no 1,5 – 3 cm. Grafiks uzņemts inercoīda kustībai pa virsmu, kur berzes spēks ir
=0,015m. Pie maziem berzes spēkiem var izmantot formulu (1.1). Tālāk aplūkojam eksperimentā iegūto līkni, kas iegūta, ja inercioīds pārvietojas vairākās taktīs. Šajā grafikā uz x-ass ir atlikts taktu (atsvaru pilnu apgriezienu periodu) skaits, kur vienas takts periods atbilst T=1,5 s. Uz y-ass atlikts vidējais pārvietojums (cm) vienā taktī, kas ir robežās no 1,5 – 3 cm. Grafiks uzņemts inercoīda kustībai pa virsmu, kur berzes spēks ir ![]() =0,07N.
=0,07N.
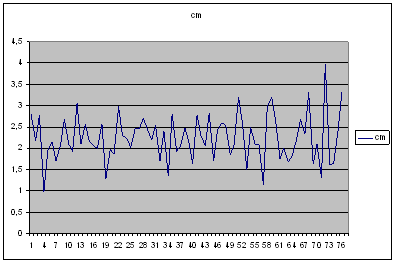
2.zīm.
2. Inercioīda vilcējspēks.
Tika veikti eksperimenti ar kravas vilkšanu uz dažādām virsmām pie atšķirīgiem berzes koeficientiem. Viena virsma bija pulēts akmens galds, bet otra abrazīva virsma. Eksperimentāli noteica berzes spēku inercioīdam ar vienu virsmu, pēc tam ar otru. Pierādījās, ka inercioīdam ir vilcējspēks. Eksperientāli noteica inercioīda berzes spēku uz abām virsmām. To skaitliskās vērtības ![]() =0,068N,
=0,068N,![]() =0,147N. Tālāk eksperimentā noteica ratiņu berzes spēku uz abām virsmām:
=0,147N. Tālāk eksperimentā noteica ratiņu berzes spēku uz abām virsmām:![]() =0,0294N,
=0,0294N,![]() =0,0686N. Zinot šos lielumus, bija iespējams noteikt rites berzes koeficientus inercioīdam un ratiņiem ar apskatāmajām virsmām:
=0,0686N. Zinot šos lielumus, bija iespējams noteikt rites berzes koeficientus inercioīdam un ratiņiem ar apskatāmajām virsmām:![]() =0,0000157m,
=0,0000157m,![]() =0,0000338m., atbilstoši
=0,0000338m., atbilstoši ![]() =0,0000333m,
=0,0000333m,![]() =0,0000777m. Šie koeficienti nepieciešami tālākos aprēķinos. Tālāk apskata sistēmu, kurā inercioīds saistīts ar ratiņiem. Sistēma atrodas miera stāvoklī, ja uz inercioīdu un ratiņiem ar kravu visi darbojošies spēki summā ir nulle. Var uzrakstīt sekojošus vienādojumus:
=0,0000777m. Šie koeficienti nepieciešami tālākos aprēķinos. Tālāk apskata sistēmu, kurā inercioīds saistīts ar ratiņiem. Sistēma atrodas miera stāvoklī, ja uz inercioīdu un ratiņiem ar kravu visi darbojošies spēki summā ir nulle. Var uzrakstīt sekojošus vienādojumus:
![]() (2.1)
(2.1)
![]() (2.2)
(2.2)
vai arī ![]() (2.3)
(2.3)
kur ![]() -vilcējspēks,
-vilcējspēks,![]() -inercioīda riteņu berzes spēks ar apskatāmajām virsmām,
-inercioīda riteņu berzes spēks ar apskatāmajām virsmām,![]() -ratiņu riteņu rites berzes koeficients ar apskatāmajām virsmām, M-ratiņu masa, m-uzkrautā smaguma uz ratiņiem masa, R-ratiņu riteņu rādiuss., g-brīvās krišanas paātrinājums. Ja uzdod skaitliskās vērtības M=0,135 kg, m=1,6kg, m=4kg, R=0,06m, g=9,81
-ratiņu riteņu rites berzes koeficients ar apskatāmajām virsmām, M-ratiņu masa, m-uzkrautā smaguma uz ratiņiem masa, R-ratiņu riteņu rādiuss., g-brīvās krišanas paātrinājums. Ja uzdod skaitliskās vērtības M=0,135 kg, m=1,6kg, m=4kg, R=0,06m, g=9,81![]() , no vienādojuma (2.3) iegūst inercioīda vilcējspēka skaitliskās vērtības uz abām virsmām
, no vienādojuma (2.3) iegūst inercioīda vilcējspēka skaitliskās vērtības uz abām virsmām ![]() . Uz abām virsmām spēki ir vienādi. Apskatam eksperimentā iegūtos grafikus:
. Uz abām virsmām spēki ir vienādi. Apskatam eksperimentā iegūtos grafikus:
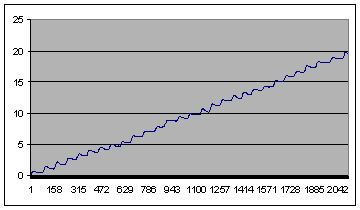
3.zīm.
Šajā grafikā redzams raksturīgais inercioīda pārvietojums, ja uz ratiņiem uzkrauts smagums 1kg. Uz x-ass atlikts laiks ms. Uz y-ass inercioīda pārvietojums cm.
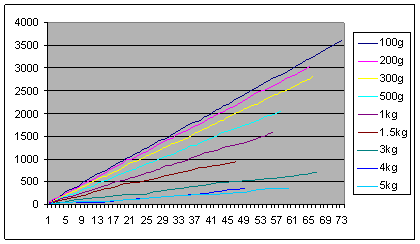
4.zīm.
Šajos grafikos attēlots inercioīda efektīvais pārvietojums, atkarībā no uz ratiņiem novietotā smaguma. No grafikiem redzams, ka pie masas m=4kg inercioīds praktiski vairs nepārvietojas.
3. Inercioīda enerģija. Saglabāšanās likums.
Līdzīgi kā iepriekšējā rakstā [1], tiek pieņemts, ka inercioīda atsvaru rotācijas enerģijas izmaiņas pāriet darbā, kas nepieciešams, lai pārvietotu inercioīda masas centru un pārvarētu berzes spēkus.
![]() (3.1)
(3.1)
Pārliecinamies,ka tas ir spēkā, ja ievietojam izteiksmē (3.1) skaitliskās vērtības. Ja ![]() un no vilcējspēka aprēķinot paātrinājumu (a=1,075
un no vilcējspēka aprēķinot paātrinājumu (a=1,075![]() , un zinot inercioīda kustības laiku vienā gājienā (uz priekšu), t=0,23s, kā arī pārvietojumu (
, un zinot inercioīda kustības laiku vienā gājienā (uz priekšu), t=0,23s, kā arī pārvietojumu (![]() , pēc formulas V=at aprēķina ātrumu, un arī kinētisko enerģiju.
, pēc formulas V=at aprēķina ātrumu, un arī kinētisko enerģiju.![]() . Līdzīgi izrēķina rotācijas enerģijas izmaiņas:
. Līdzīgi izrēķina rotācijas enerģijas izmaiņas:![]()
Apskatot inercioīda atsvaru relatīvo kustību atskaites sistēmā, kas saistīta ar inercioīda atsvariem, tad tajā eksistē inerces spēki. Atsvaru kustības kinētiskā enerģija![]() , un neinerciālā atskaites sistēmā tiek aplūkota tās izmaiņa laikā. Izmantojot teorētiskās mehānikas priekštatus [2], var noteikt pie kādiem nosacījumiem eksistē relatīvās kustības enerģijas integrālis. Ja relatīvās kustības vienādojums ir:
, un neinerciālā atskaites sistēmā tiek aplūkota tās izmaiņa laikā. Izmantojot teorētiskās mehānikas priekštatus [2], var noteikt pie kādiem nosacījumiem eksistē relatīvās kustības enerģijas integrālis. Ja relatīvās kustības vienādojums ir: ![]() , (
, (![]() -reālie spēki,
-reālie spēki,![]() -inerces spēki,
-inerces spēki,![]() -Koriolisa spēks), un ja reālie spēki atskaites sistēmā saistītiem ar rotējošiem atsvariem izsakās kā
-Koriolisa spēks), un ja reālie spēki atskaites sistēmā saistītiem ar rotējošiem atsvariem izsakās kā ![]() (kur
(kur ![]() ), tad kinētiskās enerģijas atvasinājums pēc laika ir:
), tad kinētiskās enerģijas atvasinājums pēc laika ir:![]()
![]() [2], un enerģijas integrālis
[2], un enerģijas integrālis![]() ) eksistē pie nosacījuma, ja inerces spēks
) eksistē pie nosacījuma, ja inerces spēks ![]() ir gradienta vektors [2], t.i.
ir gradienta vektors [2], t.i.
![]()
![]() (3.2)
(3.2)
vektora lauks ![]() nav virpuļains. Ja vispārīgā gadījumā vektora lauku
nav virpuļains. Ja vispārīgā gadījumā vektora lauku ![]() apraksta ar vienādojumu [2],
apraksta ar vienādojumu [2],
![]() (3.3)
(3.3)
tad lai lauks ![]() nebūtu virpuļains nepieciešami un pietiekami, lai
nebūtu virpuļains nepieciešami un pietiekami, lai ![]() [2]. Var iebilst vai pietiekami, jo problēma saistīta ar vienmērīgu rotācijas kustību. Turpretīm, ja rotācijas kustība ir nevienmērīga, tad iespējams enerģijas integrālis neeksistē un enerģijas saglabāšanās tādās sistēmās neizpildās. Lai izpildītos nosacījums (3.2), kas arī ir pamatnosacījums, var pieņemt, ka paātrinoši rotējošās sistēmās inerces spēka lauks rada pretēji cirkulējošu lauku, kuru apraksta ar vienādojumu,
[2]. Var iebilst vai pietiekami, jo problēma saistīta ar vienmērīgu rotācijas kustību. Turpretīm, ja rotācijas kustība ir nevienmērīga, tad iespējams enerģijas integrālis neeksistē un enerģijas saglabāšanās tādās sistēmās neizpildās. Lai izpildītos nosacījums (3.2), kas arī ir pamatnosacījums, var pieņemt, ka paātrinoši rotējošās sistēmās inerces spēka lauks rada pretēji cirkulējošu lauku, kuru apraksta ar vienādojumu,
![]() (3.4)
(3.4)
tādu, ka summārais lauks, no ![]() un
un![]() būtu bezvirpuļains, t.i.
būtu bezvirpuļains, t.i.
![]() (3.5)
(3.5)
Tas izpildas pie nosacījuma, ja
![]() (3.6)
(3.6)
![]()
Tas norāda, ka inerces lauks nevienmērīgi rotējošās atskaites sistēmās atstāj savu ietekmi uz ārējo Zemes gravitācijas lauku, ko var novērot inerciālā atskaites sistēmā. Līdzīgi tam kā kustošies elektriskie lādiņi rada magnētisko lauku, kas ir tikai relatīvisks efekts. Jāatzīmē, ka tālākos aprēķinos būs redzama vienādojuma (3.4) lietderība, jo inercioīda pārvietojums ir pretējs inerces spēku darbības viezienam, ko arī izsaka (3.6).
4. Spēka, kas darbojas uz inercioīda masas centru, aprēķins.
Reāla spēka izcelsme, kāds iedarbojas uz inercioīda masas centru, izrietēja no iepriekšējiem spriedumiem. Šis spēks ir saistīts ar gravitācijas lauka izmaiņām lokālā apgabalā, inercioīda atsvaru paātrinātās, palēninātās kustības dēļ. Šī iemesla dēļ rotējošie ķermeņi izmaina savu svaru [4]. Arī NEPTA projekta,”Inercioīda kustības pētījumi” ietvaros tika veikts eksperiments par inercioīda svara izmaiņu tā darbības laikā. Tika novērotas svara izmaiņas. Tās bija niecīgas, un lielākai pārliecībai nepieciešami papildus eksperimenti. Neskatoties uz tādiem trūkumiem, izmantojot iepriekšējo sadaļu, no vienādojuma (3.4) var noteikt spēka ![]() x-to komponenti. Šim nolūkam no vienādojuma(3.4) izsaka rotora z-to komponenti:
x-to komponenti. Šim nolūkam no vienādojuma(3.4) izsaka rotora z-to komponenti:
![]() (4.1)
(4.1)
Ņemot vērā, ka ![]() un
un ![]() , [1] vienādojumu (4.1) pārveido
, [1] vienādojumu (4.1) pārveido
![]() (4.2)
(4.2)
T width=17ā kā ![]() un
un ![]() , iegūstam integrāli
, iegūstam integrāli
![]() (4.3)
(4.3)
Integrāli var atrisināt vai nu izmantojot integrāļu tabulas, vai arī izvirzot ![]() pakāpju rindā (
pakāpju rindā (![]() . Iegūstam, ka
. Iegūstam, ka
![]() +C (4.4)
+C (4.4)
kur ![]() leņķiskais paātrinājums, C-integrēšanas konstante. Šī izteiksme pilnīgi atbilst izteiksmei par spēku, kāds darbojas uz inercioīda masas centru, cita autora darbā [4]. Analoģisku izteiksmi iegūst, ja izmanto cos izvirzījumu.
leņķiskais paātrinājums, C-integrēšanas konstante. Šī izteiksme pilnīgi atbilst izteiksmei par spēku, kāds darbojas uz inercioīda masas centru, cita autora darbā [4]. Analoģisku izteiksmi iegūst, ja izmanto cos izvirzījumu.
![]() (4.5)
(4.5)
Zinot integrēšanas konstantes skaitlisko vērtību ![]() un pārējos apskatāmā inercioīda parametrus ir iegūstama spēka, kurš darbojas uz inercioīda masas centru skaitliskā vērtība:
un pārējos apskatāmā inercioīda parametrus ir iegūstama spēka, kurš darbojas uz inercioīda masas centru skaitliskā vērtība: ![]() . Šī spēka skaitliskā vērtība sakrīt ar iepriekš iegūto inercioīda vilcējspēka skaitlisko vērtību, kura:
. Šī spēka skaitliskā vērtība sakrīt ar iepriekš iegūto inercioīda vilcējspēka skaitlisko vērtību, kura:![]() . Pēc šādas sakritības var secināt, ka cirkulējošs inerces spēka lauks rada sev pretēji cirkulējošu lauku.
. Pēc šādas sakritības var secināt, ka cirkulējošs inerces spēka lauks rada sev pretēji cirkulējošu lauku.
5. Nobeigums un secinājumi.
Šajā rakstā ir iegūtas spēka, kurš darbojas uz inercioīda masas centru, skaitliskās izteiksmes, kā arī noteikta tā skaitliskā vērtība. Tika arī noskaidrota šā spēka izcelsme. Tas, ka inerces spēka lauks spēj radīt sev pretēji cirkulējošu lauku, spējīgu iedarboties lokāli uz Zemes gravitācijas lauku, tika daļēji konstatēts NEPTA projekta ”par inercioīda kustības pētījumiem” eksperimentos. Tika noteikta ārējā gravitācijas lauka intensitātes izmaiņa inercioīda darbības laikā. Tā eksperimentālā korekcija bija ![]() . Turpretīm, ja teorētiski pieņem, ka inercioīda paātrinājums, kura skaitliskā vērtība
. Turpretīm, ja teorētiski pieņem, ka inercioīda paātrinājums, kura skaitliskā vērtība ![]() , atbilst lokāli izmainītā gravitācijas lauka intensitātes x-ai komponentei, tad gravitācijas lauka intensitātes izmaiņa atbilstu lielumam, kas arī tuva eksperimentālajai. Protams ir nepieciešami vairāk mērījumi, kā arī jāuzlabo eksperimenta kvalitāte. Ja šāda koncepcija atbilst realitātei, tad inercioīda masas centra kustību varētu skaidrot kā tā brīvo krišanu gravitācijas spēka laukā pa tā x-to komponenti, kāda reālos apstākļos nepastāv, jo gravitācijas spēks vienmēr vērsts uz Zemes centru. Neskatoties uz šādu secinājumu, nedrīkst ignorēt citu autoru pētījumus. Tā piemēram pētījumi par to, ka rotējoši ķermeņi ģenerē mākslīgu centrtieces gravistarojumu [5], kas arī varētu būt cēlonis žiroskopiskam efektam, pēc kura tiek realizēta bezatbalsta inerces kustība. Līdzīgi var norādīt eksperimentus pēc kuriem noskaidrots rotējošo masu mainīga kvadrupolā momenta starojuma spiediens uz cietiem ķermeņiem vakuumā [6]. Vēl var norādīt eksperimentu, NEPTA projekta ietvaros, ka inercioīda pārvietojums nav atkarīgs no rotējošo atsvaru materiāla. Tā piemēram 5.zīm. redzami pārvietojumu grafiki ar svina un stikla rotējošā mehānisma atsvariem.
, atbilst lokāli izmainītā gravitācijas lauka intensitātes x-ai komponentei, tad gravitācijas lauka intensitātes izmaiņa atbilstu lielumam, kas arī tuva eksperimentālajai. Protams ir nepieciešami vairāk mērījumi, kā arī jāuzlabo eksperimenta kvalitāte. Ja šāda koncepcija atbilst realitātei, tad inercioīda masas centra kustību varētu skaidrot kā tā brīvo krišanu gravitācijas spēka laukā pa tā x-to komponenti, kāda reālos apstākļos nepastāv, jo gravitācijas spēks vienmēr vērsts uz Zemes centru. Neskatoties uz šādu secinājumu, nedrīkst ignorēt citu autoru pētījumus. Tā piemēram pētījumi par to, ka rotējoši ķermeņi ģenerē mākslīgu centrtieces gravistarojumu [5], kas arī varētu būt cēlonis žiroskopiskam efektam, pēc kura tiek realizēta bezatbalsta inerces kustība. Līdzīgi var norādīt eksperimentus pēc kuriem noskaidrots rotējošo masu mainīga kvadrupolā momenta starojuma spiediens uz cietiem ķermeņiem vakuumā [6]. Vēl var norādīt eksperimentu, NEPTA projekta ietvaros, ka inercioīda pārvietojums nav atkarīgs no rotējošo atsvaru materiāla. Tā piemēram 5.zīm. redzami pārvietojumu grafiki ar svina un stikla rotējošā mehānisma atsvariem.
Autors izsaka pateicību projekta vadītājam G.Māliņam par ieteikumiem un kritiku,kā ai ekasperimentālajiem datiem. 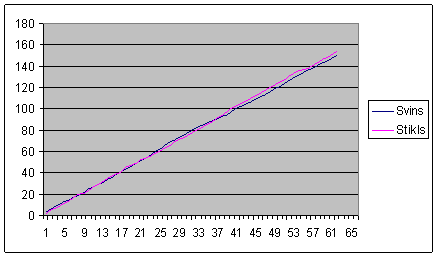
5.zīm.
Literatūra.
1. P.Linkēvičs. V.Tolčina inercioīda masas centra kustības īpatnību interpretācija. www.nepta.lv
2. В.Г.Невзглядов. Теоретическая механика. гос.издат.физ.-мат.лит.М.1959
3. В.Н.Толчин. Инерциоид. Пермь:Перм.кн.из.1977
4. Гаухман М.Х. Алгебра сигнатур
5. Бостоцкий.Ю.Г. Способы генерирования искуственного гравитационного излучения. доклад на международной конференции «Новые идеи в естествознании» Санкт-Петербург.1996г.
6. В.Н.Самахвалов. Давление квадрупольного излучения вращающихся масс на тведие тела
P.Linkēvičs
NEPTA
www.nepta.lv
2012.gada marts.



